A Hamilton-Jacobi-based Proximal Operator
Stanley Osher, Howard Heaton, and Samy Wu Fung
Summary
We give a formula for estimating proximal operators from (possibly noisy) observations of objective function values.
Key Steps
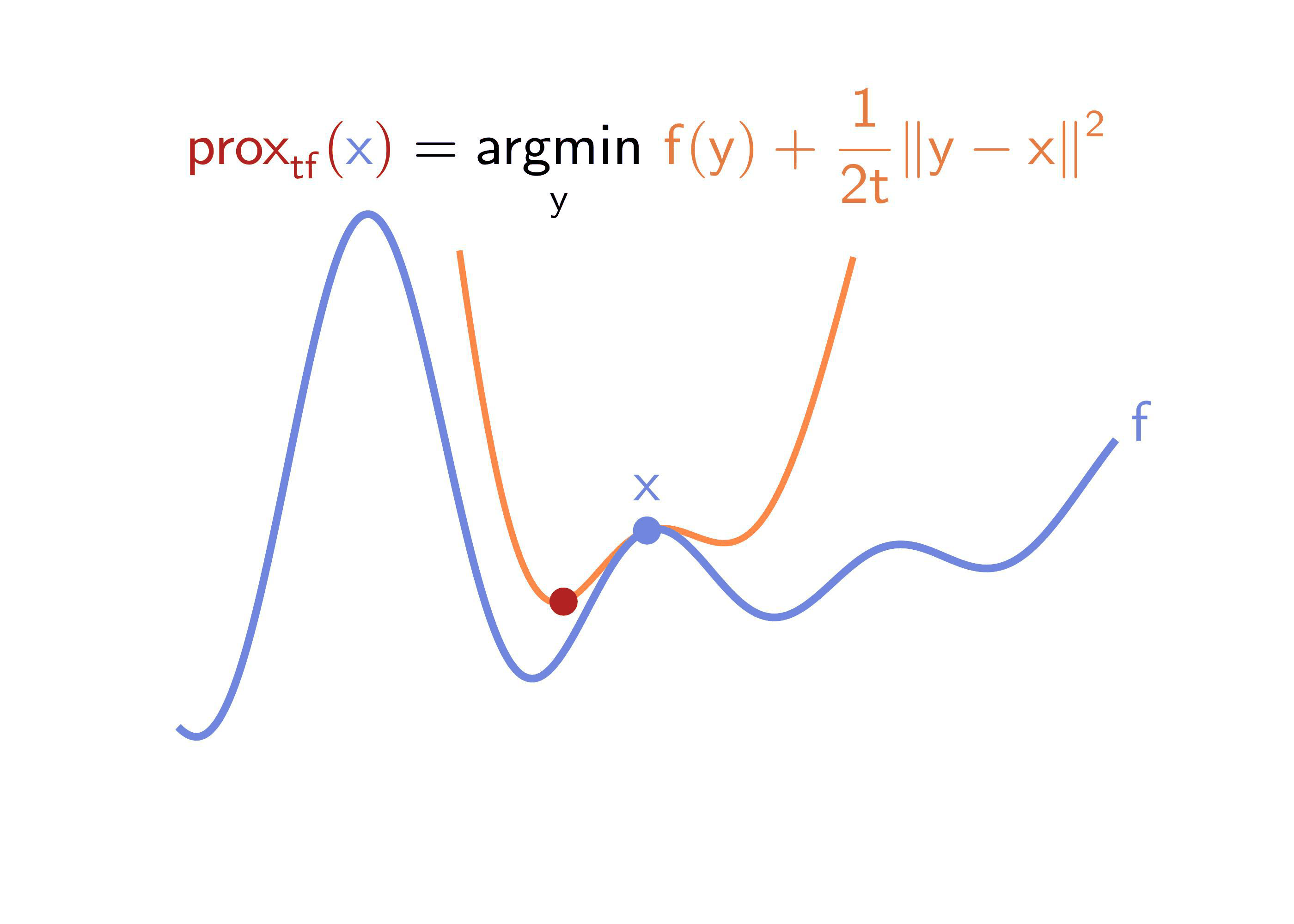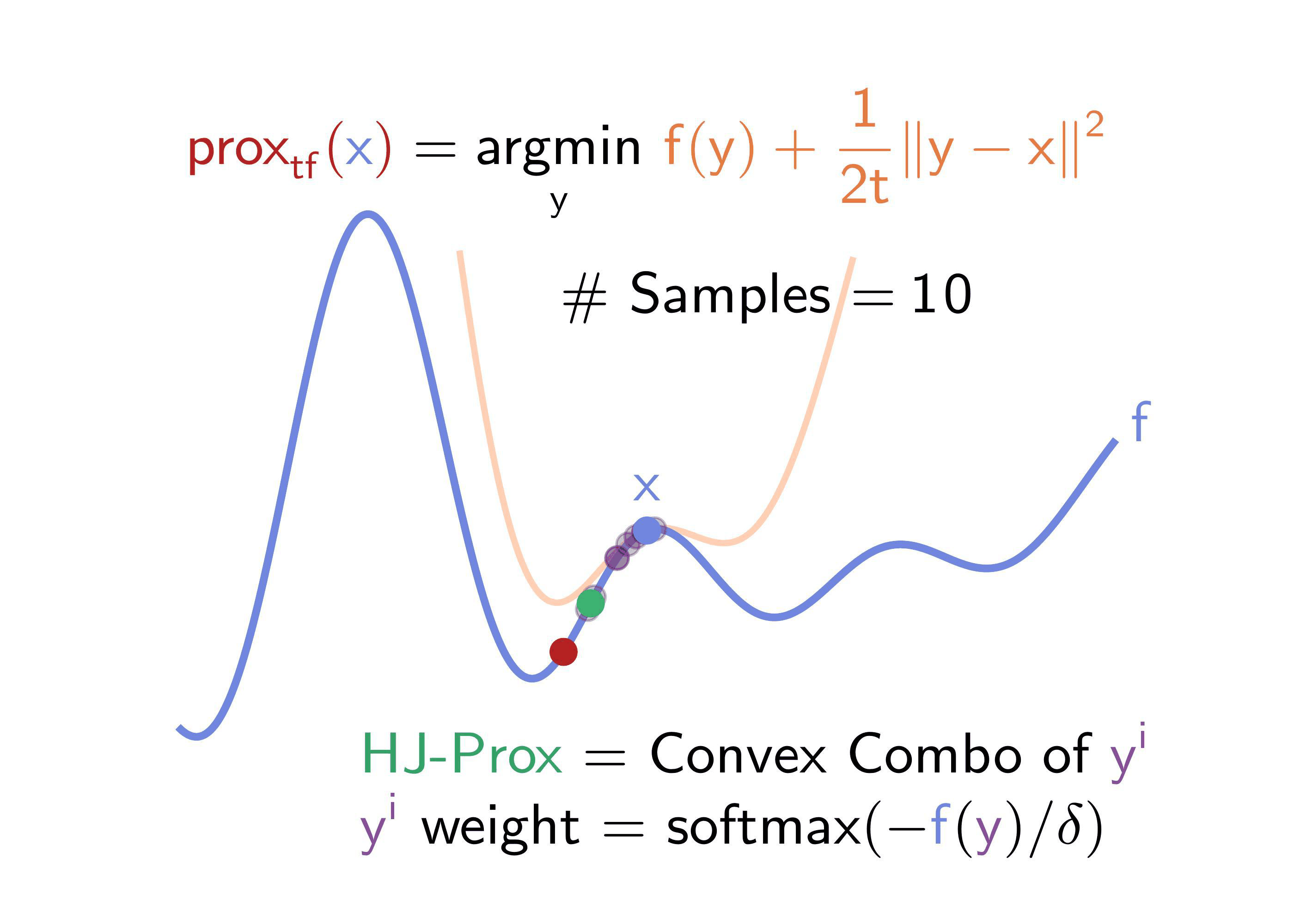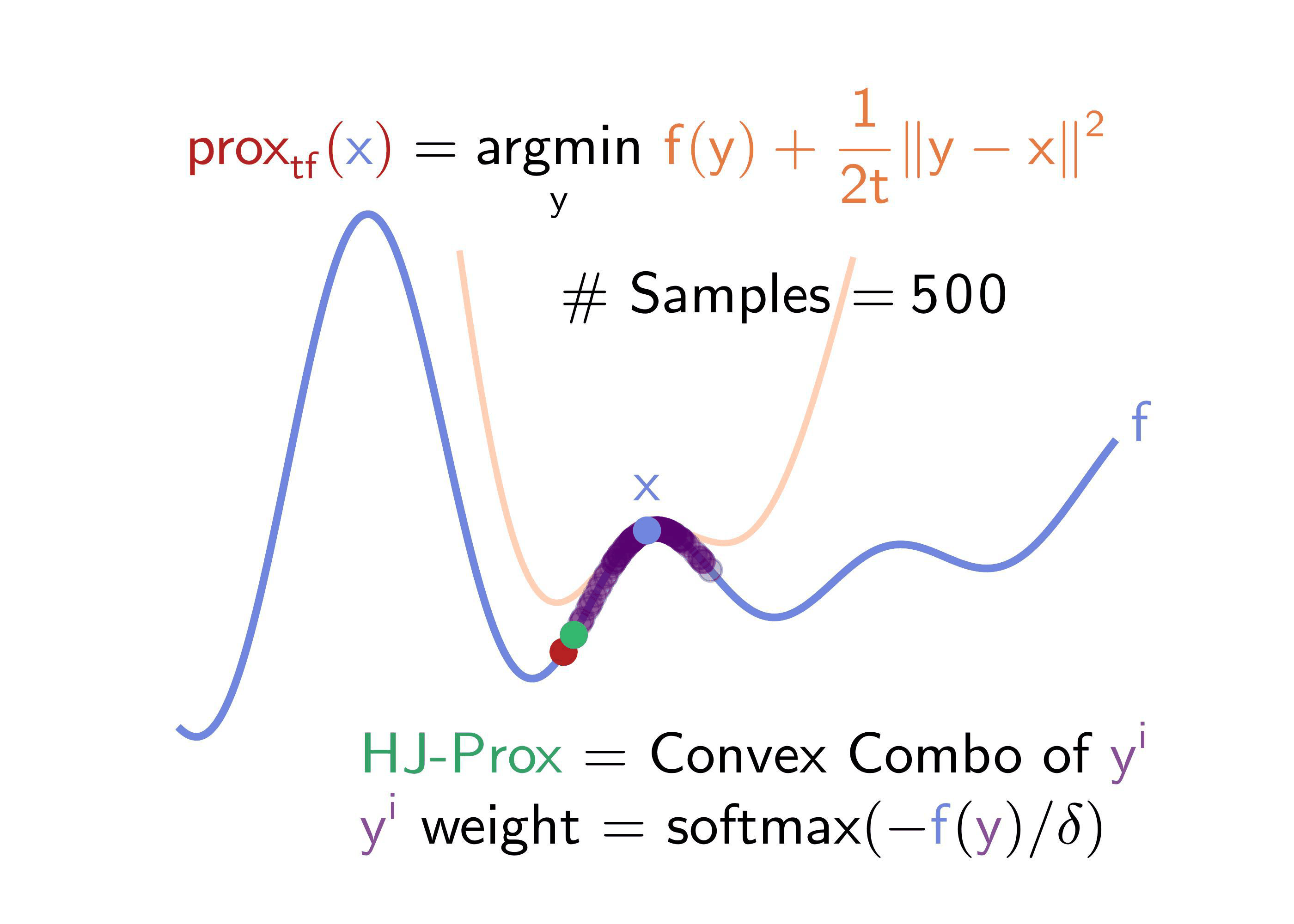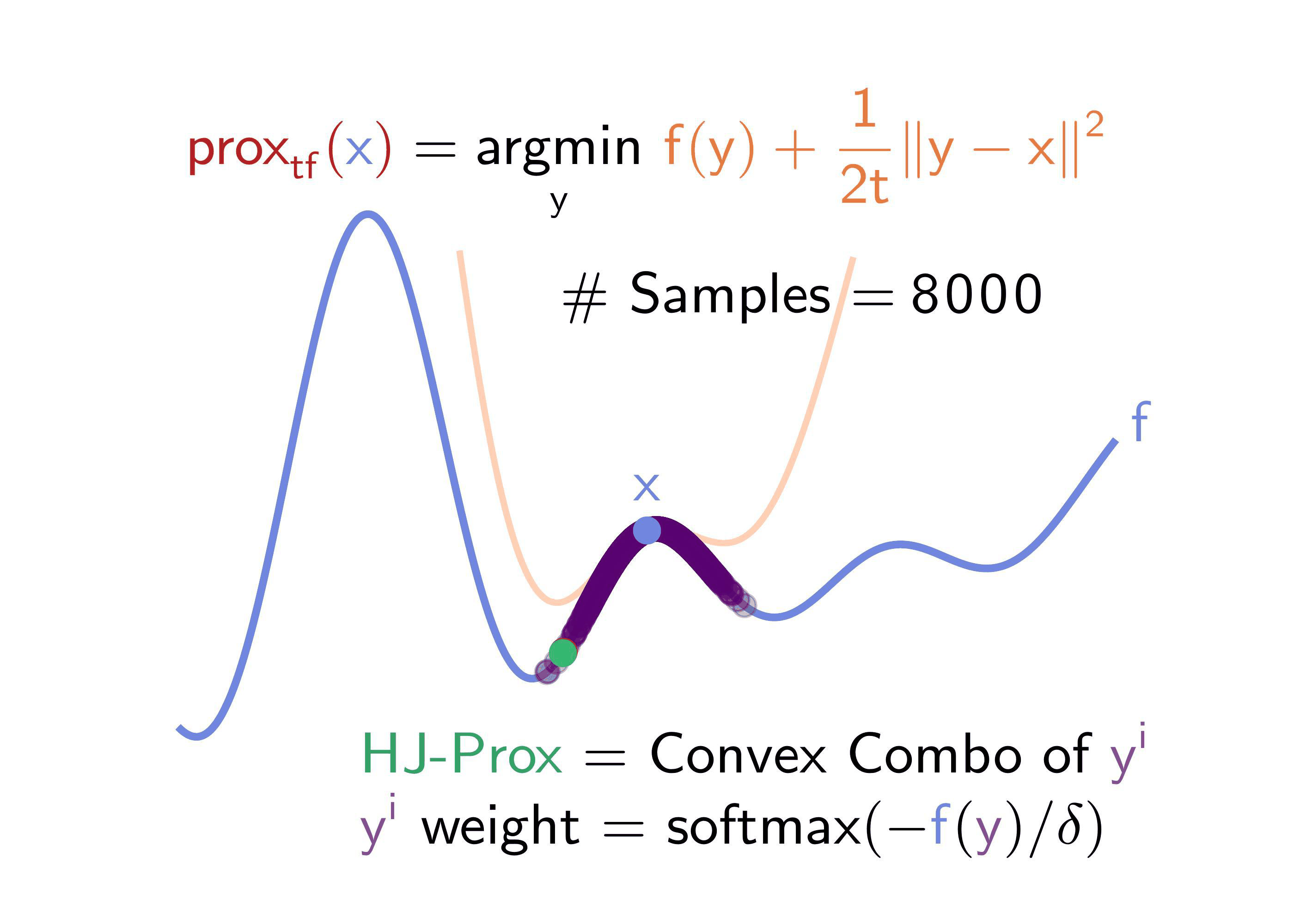
- Sample points \(\mathsf{y^i}\) (via a Gaussian) about the input \(\mathsf{x}\)
- Evaluate function \(\mathsf{f}\) at each point \(\mathsf{y^i}\)
- Estimate proximal by using softmax to combine the values for \(\mathsf{f(y^i)}\) and \(\mathsf{y^i}\)
Abstract
First-order optimization algorithms are widely used today. Two standard building blocks in these algorithms are proximal operators (proximals) and gradients. Although gradients can be computed for a wide array of functions, explicit proximal formulas are known for only limited classes of functions. We provide an algorithm, HJ-Prox, for accurately approximating such proximals. This is derived from a collection of relations between proximals, Moreau envelopes, Hamilton–Jacobi (HJ) equations, heat equations, and Monte Carlo sampling. In particular, HJ-Prox smoothly approximates the Moreau envelope and its gradient. The smoothness can be adjusted to act as a denoiser. Our approach applies even when functions are accessible only by (possibly noisy) black box samples. We show that HJ-Prox is effective numerically via several examples.
Citation
